一个数知识题终于处分了，这个问题描画了不错放在旯旮里的最大尺寸的沙发文爱 app，尽管它可能无法匡助你迁移。

在《石友记》中，一位数学家天然晚了二十五年才匡助罗斯将他的新沙发搬进他的公寓，但他终于处分了令东说念主敌视的“沙提问题”。"

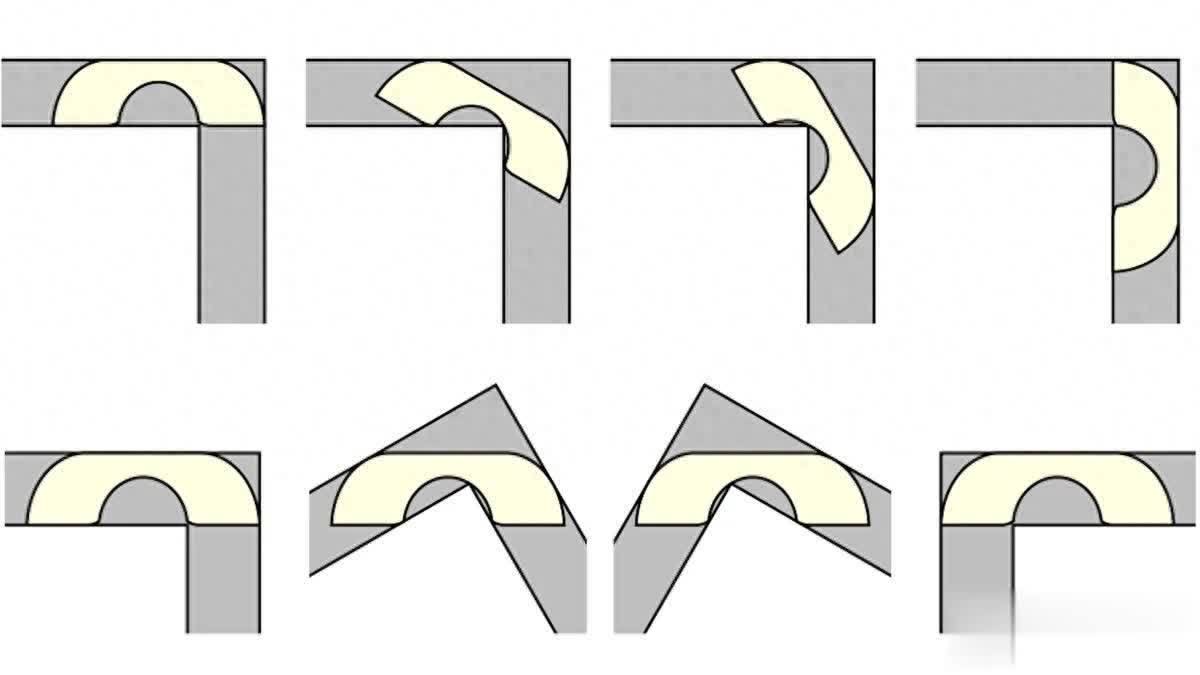
这说念数学题描画了在给定宽度的旯旮里能放得下的最大沙发尺寸 —— 这恰是1999年播出的《石友记》中一集里的东说念主物所濒临的问题。事实证据，要是罗斯能接头一下有18个弧线部分、最大面积为2.2195个单元的格弗沙发，他的“旋转”就不错幸免了。（好吧，也许它不会有那么大的匡助。）

沙提问题的处分在数学上是第一次。这个问题是由奥地利-加拿大数学家Leo Moser在1966年提倡的。Moser条目在一个平面上，单个体式的最大可能区域不错在单元宽度为1的走廊直角角周围迁移。天然这看起来很通俗，但数学畸形复杂文爱 app，因为这个问题波及面积最大化和体式的迁移。

刻下，韩国延世大学（Yonsei University）数学博士后接头员白吉宁（Jineon Baek）找到了谜底。白阐扬于12月2日在预印本网站ArXiv上发布了他的处分决议。在100多页的数学证据中，白阐扬发现，对于一个宽度为1个单元的走廊，思象中的沙发的最大面积不错是2.2195个单元 —— 从之前已知的2.2195到2.37个单元的界限精准地收缩了谜底。这一证据尚未在同业评议的期刊上发表，还需要其他数学家进行接头，以详情它如实是最优的。

格弗沙发上的“格弗”是罗格斯大学的名誉阐扬、数学家约瑟夫·格弗，他在1992年提倡了2.2195的下界。但对于沙发是否不错更大的问题一直存在争议，2018年的一个团队使用打算机赞助证据标明，2.37内容上是上限。

格弗的沙发是一张宽大的U形沙发，有一个弧形的“座椅”，不错挤在旯旮里而不会被挂起来。 问题是，这张经心遐想的沙发--由18个孤独的弧线组合在一皆制成 —— 是否确切是不错转弯的最大、最理思的体式。 贝克接头了体式的几何体式卓越通顺，发现格弗的处分决议内容上是正确的。

这一凭据在搪塞媒体上引起了鄙俗宽恕。

用户@morallawwithin于12月6日在搪塞平台X上写说念：“这是最理思的沙发”文爱 app，并发布了一张畸形宽的扶手沙发体式的相片。“你可能不心爱它，但这即是峰值优化的模式。”